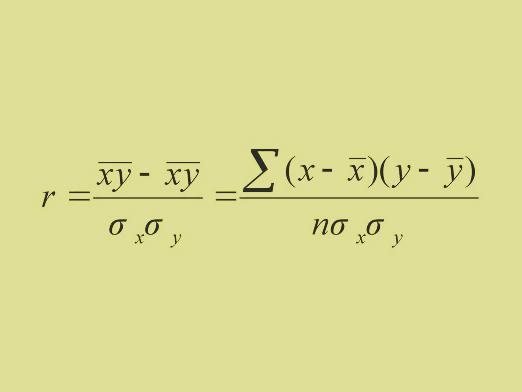Kaip rasti nuolydį?

Matematika - vienas iš parametrų, apibūdinančiųlinijos pozicija Dekarto koordinačių plokštumoje yra šios linijos nuolydis. Šis parametras apibūdina tiesios linijos nuolydį į abscisu ašį. Norint suvokti, kaip rasti kampinį koeficientą, pirmiausia mes primename bendrą XY koordinačių sistemos tiesinės linijos lygtį.

Apskritai bet kuri eilutė gali būti išreikšta išraiška ax + į = c, kur a, b ir c yra savavališkai realūs skaičiai, bet² + b² ≠ 0.

Panaši lygtis su paprasta pagalbatransformacijos gali būti pateikiamos į formą y = kx + d, kurioje k ir d yra tikri skaičiai. K skaičius yra kampinis koeficientas, o tokios tiesios linijos lygtis vadinama lygtimi su kampiniu koeficientu. Pasirodo, kad norint rasti kampinį koeficientą, tiesiog reikia pateikti originalią lygtį aukščiau pateiktai formai. Norėdami išsamiau suprasti, apsvarstykite konkretų pavyzdį:

Problema: raskite linijos nuolydį, pateiktą lygtimi 36x - 18y = 108

Sprendimas: paverčiame pradinę lygtį.

36x - 18y = 108

18y = 36x - 108

y = 2x - 6

Atsakymas: reikiamas šios linijos kampinis koeficientas yra 2.

Jei transformacijos lygtyje mesgavo išraišką tipo x = const ir todėl negali parodyti y kaip x funkcija, tada mes susiduriame su tiesia linija, lygiagreti X ašiai. Tokios linijos kampinis koeficientas yra lygus begalybei.

Linijoms, kurios išreiškiamos lygtimi tipo y = const, nuolydis yra lygus nuliui. Tai būdinga tiesiosioms linijoms, lygiagrečioms su abscisių ašimi. Pavyzdžiui:

Problema: rasti linijos nuolydį, pateiktą lygtimi 24x + 12y-4 (3y + 7) = 4

Sprendimas: sumažiname pradinę lygtį prie bendrosios formos

24x + 12y - 12y + 28 = 4

24x = 28 - 4

x = -1

Neįmanoma išreikšti y iš gautos išraiškos, taigi nurodytos linijos nuolydis yra begalybė, o pati linija yra lygiagreti Y ašiai.

Geometrinė reikšmė

Norint geriau suprasti, pažvelkime į paveikslėlį:

Paveiksle matome funkcijos y = kx funkcijos grafiką. Paprastumui imkime koeficientą c = 0. Trikampio OAB atveju BA pusės santykis su AO bus lygus kampiniam koeficientui k. Tuo pačiu metu santykis BA / AO yra ūminio kampo α kakliukas dešiniajame kampe trikampio OAB. Pasirodo, kad tiesios linijos kampinis koeficientas yra lygus kampo, ty šios linijos su tinklelio abscisu ašimi, tašką.

Problemos sprendimas, kaip rasti nuolydįtiesiai, randame kampo tarpusį ir koordinačių tinklelio x ašies tangentą. Ribiniai atvejai, kai nagrinėjama tiesa yra lygiagreti koordinačių ašims, patvirtina aukščiau. Tiesą sakant, tiesia linija, aprašyta lygtimi y = const, kampas tarp jo ir abscisu ašies yra lygus nuliui. Nulinio kampo tangentas taip pat yra nulis, o nuolydis taip pat yra nulis.

Tiesia linijoms, statmenoms abscisu ašiai irapibūdinama lygtimi x = const, kampas tarp jų ir ašies X yra 90 laipsnių. Teisingo kampo tangentas yra lygus begalybei, taigi tokių linijų kampinis koeficientas yra lygus begalybei, o tai patvirtina tai, kas parašyta aukščiau.

Tangento kampinis koeficientas

Dažnas, dažnaspraktika, užduotis taip pat yra nustatyti tam tikro momento funkcijos grafiko tangento kampinį koeficientą. Tangentinė linija yra tiesi linija, todėl jai taikomas ir kampinio koeficiento sąvoka.

Suprasti, kaip rasti nuolydįTangentiška, turime prisiminti išvestinės priemonės sąvoką. Bet kokios funkcijos išvestinė dalis tam tikru momentu yra pastovi skaičiuoklė, lygi kampo, esančio taške, esančiame nurodytame taške, su šios funkcijos grafiku ir abscisu ašimi. Pasirodo, kad nustatyti taško x tangento kampinį koeficientą₀, mes turime apskaičiuoti pradinės funkcijos išvesties vertę šiame taške k = f "(x₀) Apsvarstykite pavyzdį: