Kaip rasti trapecijos aukso?

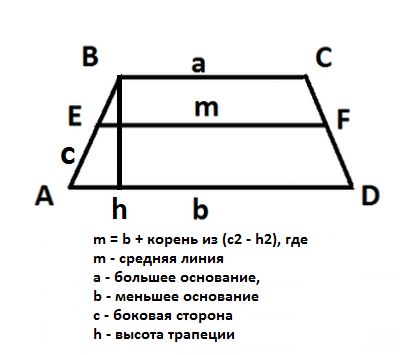
Trapecijos yra keturkampis, dukurių kraštinės yra lygiagrečios (tai yra trapecijos pagrindai, nurodyti a ir b paveikslėliais), o kiti du nėra (figūroje, AD ir CB). Trapecijos aukštis yra segmentas h, patrauktas statmenai pagrindams.
Kaip rasti trapecijos pločio ir pagrindo ilgio trapecijos aukštį?

Norėdami apskaičiuoti trapecijos ABCD sritį S, naudokime šią formulę:
S = ((a + b) × h) / 2.
Čia a ir b segmentai yra trapecijos pagrindai, h - trapecijos aukštis.
Konvertavę šią formulę galime parašyti:
h = 2 × S / (a + b)
Naudodamiesi šia formule mes gauname h reikšmę, jei žinoma sritis S ir pagrindų a ir b ilgis.
Pavyzdys:
Jei žinoma, kad trapecijos S plotas yra 50 cm², pagrindo a ilgis yra 4 cm, bazės b ilgis yra 6 cm, tada aukščio h nustatymui naudojama formulė:
h = 2 × S / (a + b);
Mes pakeičiame žinomus kiekius į formulę.
h = (2 × 50) / (4 + 6) = 100/10 = 10 cm
Atsakymas: trapecijos aukštis yra 10 cm.
Kaip nustatyti trapecijos aukštį, jei yra trapecijos laukas ir vidurinės linijos ilgis?

Mes naudojame trapecijos srities apskaičiavimo formulę:
S = m × h
Čia m yra vidurinė linija, h yra trapecijos aukštis.
Jei kyla klausimas, kaip rasti trapecijos aukštį, formulė:
h = S / m, bus atsakymas.
Taigi, mes galime rasti trapecijos h aukštį, žinant sritis S ir vidurinės linijos segmentą m.
Pavyzdys:
Yra žinomas trapecijos m vidurinės linijos ilgis, kuris yra 20 cm, o sritis S - 200 cm2. Leiskite mums rasti trapecijos h aukščio vertę.
h = S / m.
Pakeičiant S ir m vertes, mes gauname:
h = 200/20 = 10 cm
Atsakymas: trapecijos aukštis yra 10 cm
Kaip rasti stačiakampio trapecijos aukštį?

Jei trapecija yra keturkampis, su dviemlygiagrečiai trapecijos šonai (bazės). Įstrižainė yra segmentas, jungiantis du priešingus trapecijos kampų viršūnius (segmentas AC, esantis paveikslėlyje). Jei trapecija yra stačiakampė, naudojant įstrižainę, mes nustatome trapecijos h aukštį.
Stačiakampio trapecija yra trapecija, tokia, kad viena iš šoninių pusių yra statmena pagrindams. Tokiu atveju jo ilgis (AD) sutampa su aukščiu h.
Taigi, apsvarstykite stačiakampio trapecijos ABCD,kur AD yra aukštis, DC yra bazė, AC yra įstrižainė. Mes naudojame Pythagorean teoremą. Stačiakampio trikampio ADC hipotenelio kvadratas yra lygus jo kojų AB ir BC kvadratų skaičiui.
Tada mes galime parašyti:
AC² = AD² + DC².
AD yra trikampio kateteris, trapecijos puse ir tuo pačiu jo aukštis. Galų gale segmentas AD yra statmenas bazėms. Jo ilgis bus:
AD = √ (AC² - DC²)
Taigi, mes turime trapecijos h = AD aukščio skaičiavimo formulę
Pavyzdys:
Jei stačiakampio trapecijos (DC) pagrindo ilgis yra 14 cm, o įstrižainė (AC) yra 15 cm, mes turėsime naudoti Pythagorean teoremą, kad gautume aukštį (AD pusė).
Tegul x yra nežinoma kojelė dešiniajame trikampyje (AD), tada
AC² = AD² + DC² gali būti užregistruotas
15² = 14² + ²²,
x = √ (15²-14²) = √ (225-196) = √29 cm
Atsakymas: stačiakampio trapecijos (AB) aukštis bus √29 cm, kuris yra maždaug 5,355 cm
Kaip rasti vienodo laipsnio trapecijos aukštį?
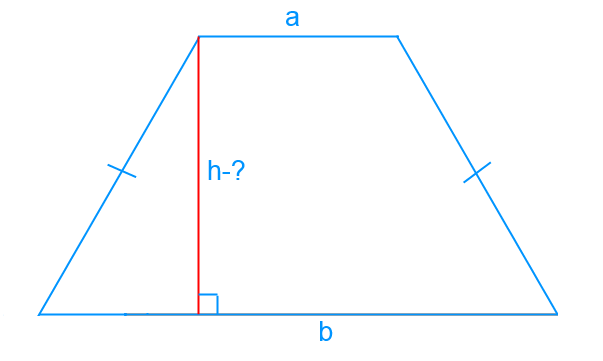
Pusiausvyros trapecijos yra vadinamas trapecijos, yŠoninių pusių ilgiai vienodi. Tiesia linija, pritvirtinta per tokio trapecijos bazių vidurį, bus simetrijos ašis. Konkretus atvejis yra trapecija, kurios įstrižainės yra statmenos viena kitai, tada aukštis h bus lygus pusei bazių sumos.
Pažvelkime į atvejį, jei nėra įstrižainiųyra statmenos viena kitai. Vienalytėje (lygiaverčioje) trapecijos srityje kampai bazėse ir įstrižainių ilgiai yra vienodi. Taip pat žinoma, kad visi vienodo šoninio trapecijos viršūnės prisiliesti prie šio trapecijos pritrauktos apskritimo linijos.
Apsvarstykite piešinį. ABCD yra lygiagreti trapecija. Ji yra žinoma, kad trapecijos lygiagrečių priemonėmis bazę, BC = b lygiagrečiai AD = a, pusė AB "= kompaktinio = c, tai, dėl kurių bazių kampai atitinkamai, gali būti parašyta kampas BAQ = CDS = α, ir kampas ABC = BCD = ß. Taigi, mes darome išvadą, kad trikampis ABQ yra lygus trikampio SCD, taigi segmentas
AQ = SD = (AD-BC) / 2 = (a-b) / 2.
Atsižvelgiant į problemos būklę bazių a ir b vertybes ir šoninės pusės c ilgį, mes nustatome, kad trapecijos aukštis h yra lygus segmentui BQ.
Apsvarstykite dešinį trikampį ABQ. IN - į trapecijos aukščio statmena AD bazę, taigi segmento AQ. Šoninio AQ trikampio ABQ, randame, naudodami anksčiau gautą formulę:
AQ = (a - b) / 2.
Su dviejų kojų stačiojo trikampio vertybes, įžambinė rasite BQ = H. Naudokite Pitagoro teorema.
AB² = AQ² + BQ²
Mes pakeičiame užduoties duomenis:
C² = AQ² + h².
Gauta formulė, skirta rasti vienodo laipsnio trapecijos aukštį:
h = √ (c²-AQ²).
Pavyzdys:
Atsižvelgiant į vienarūšę trapecijos ABCD, kur bazėAD = a = 10cm, bazė BC = b = 4cm, o šoninė AB = c = 12cm. Tokiomis sąlygomis leiskite mums apsvarstyti, pvz., Kaip rasti trapecijos aukštį, lygiagrečią ABCD trapeciją.
Mes randame ABQ trikampio AQ pusę, pakeičiant žinomus duomenis:
AQ = (A - B) / 2 = (10-4) / 2 = 3cm.
Dabar pakeiskite trikampio pusių vertes formoje Pythagorean teorema.
h = √ (c²- AQ²) = √ (12² - 3 ²) = √135 = 11,6 cm.
Atsakymas. Dvigubo trapecijos ABCD aukštis h yra 11,6 cm.