Kaip rasti parabolę?

Parabola yra kvadratinės funkcijos grafikas. Ši eilutė turi reikšmingą fizinę prasmę. Kad būtų lengviau rasti parabolos viršūnę, ją reikia nubrėžti. Tada ant diagramos galite lengvai pamatyti viršutinę dalį. Tačiau siekiant parabolos reikia žinoti, kaip rasti parabolų taškus ir kaip rasti parabolų koordinates.
Rasime taškus ir parabolos viršūnę
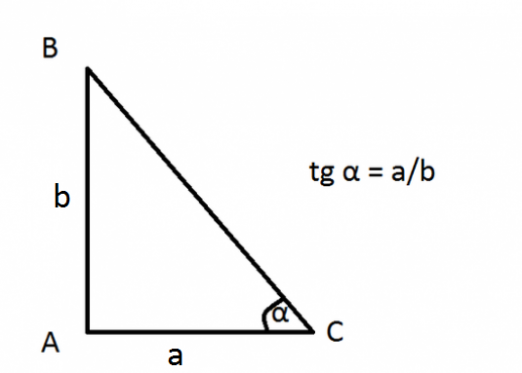
Bendrame reprezentacijoje kvadratinė funkcija turi tokią formą: y = ax2+ bx + c. Šios lygties grafikas yra parabola. Jei a> 0, jo šakos nukreiptos į viršų, o jei <0 - žemyn. Norėdami parabolą pastatyti ant grafiko, reikia žinoti tris taškus, jei jis eina išilgai ordinato ašies. Priešingu atveju reikėtų žinoti keturis statybos taškus.
Kai randate abscisę (x), reikia iš koeficiento (x) atsižvelgti iš pateiktos polinomos formulės, o po to du kartus padalyti koeficientą (x2), tada padauginkite iš skaičiaus - 1.
Norėdami rasti reikia rasti diskriminantinę nacionalines nuostatas, ir tada padauginkite jį - 1, ir tada dalijama iš (x koeficiento2), pirmiausia ją padauginus iš 4.
Be to, skaičiuojamų verčių pakeitimas apskaičiuojamasviršūnių parabolės formos. Dėl visų skaičiavimų pageidautina naudoti mokslinį skaičiuotuvą, ir piešimo parabolė grafiką ir naudoti liniuotę ir lyumografom, ji bus žymiai pagerinti savo skaičiavimus tikslumą.
Apsvarstykite šį pavyzdį, kuris padės suprasti, kaip rasti parabolos viršūnę.
x2-9 = 0. Šiuo atveju viršūnės koordinatės apskaičiuojamos taip: 1 taškas (-0 / (2 * 1), taškas 2 - (0 ^ 2-4 * 1 * (-9)) / (4 * 1)). Taigi, viršūnės koordinatės yra vertės (0, 9).
Raskite viršūnės abscisu
Kai sužinojau, kaip rasti parabolė, ir gali apskaičiuoti savo sankirtoje su koordinačių ašimi (x), mes galime lengvai apskaičiuoti smailių abscisių.
Tarkime, kad (x1) ir (x2) yra parabolos šaknys. Parabolės šaknys yra jos sankirtos su abscisu ašimi taškai. Šios vertės nukreipia į nulį tokios formos kvadratiną lygtį: ax2 + bx + c.
Šiuo atveju | x2| | | > | x1|, tada parabolos viršūnė yra viduryje tarp jų. Taigi, jis gali būti toks: x0 = ½ (| x2| | | - | x |1|)
Raskite figūros sritį
Norėdami rasti figūros plotą koordinatejums reikia žinoti integralą. Ir jį taikyti, pakanka žinoti tam tikrus algoritmus. Norint rasti parabolių ribas apibūdintą plotą, būtina pateikti jo vaizdą Dekarto koordinačių sistemoje.
Pirma, pagal aukščiau aprašytą metodąašies (x) viršūnės koordinatė, tada ašis (y), po kurios yra parabolos viršūnė. Dabar turime nustatyti integracijos ribas. Paprastai jie nurodomi problemos būklėje naudojant kintamuosius (a) ir (b). Šios vertės turėtų būti dedamos atitinkamai viršutinėje ir apatinėje integralo dalyse. Tada įveskite bendrosios formos funkcijos vertę ir padauginkite ją (dx). Parabolės atveju: (x2) dx.
Tada turime bendrai apskaičiuoti antidekvatusfunkcijos vertė. Norėdami tai padaryti, naudokite specialią vertybių lentelę. Pakeičiant integracijos ribas, yra skirtumas. Šis skirtumas bus plotas.
Pavyzdžiui, apsvarstykite lygčių sistemą: y = x2+1 ir x + y = 3.
Yra susikirtimo taškų abscisai: x1= -2 ir x2= 1
Mes manome, kad y2= 3, o y1= x2 + 1, pakeiskite vertes aukščiau pateiktoje formulėje ir gaukite 4,5 vertės.
Dabar išmokome rasti parabolę, o remiantis šiais duomenimis, apskaičiuojame paveikslo plotą, kurį jis apriboja.