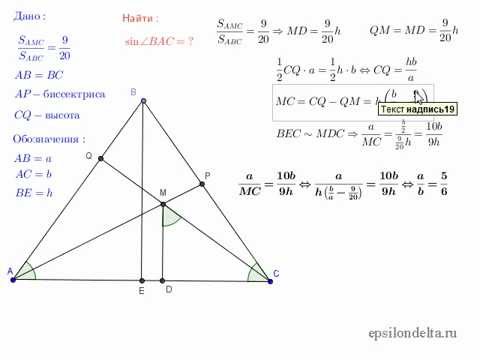
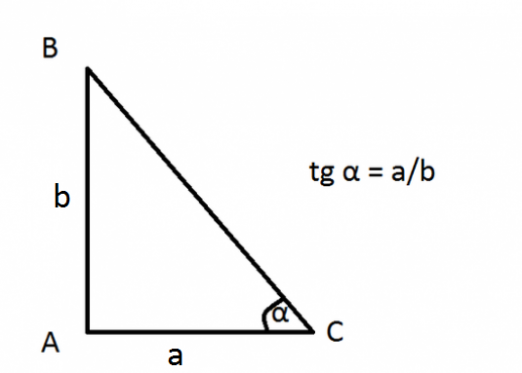
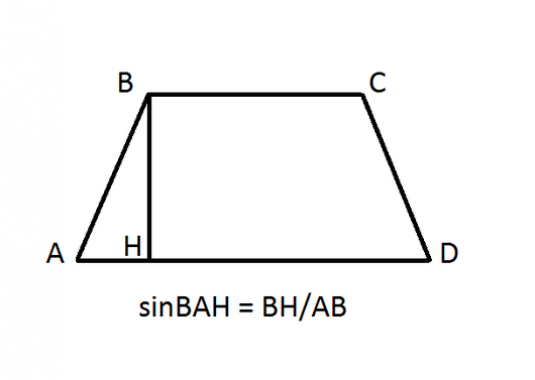
Kaip rasti trikampio kampo sinusą?

Norėdami surasti stačiakampio trikampio kampo sinusą, turime prisiminti, kas yra sinusas pagal apibrėžimą. Ir apibrėžimas yra labai paprastas: kampo sinusas yra lygus priešingos kojos ir hipotenelio santykiui.

Kaip apskaičiuoti sines

Jei turime trikampį ABC, kurio A -teisingas kampas, tada šonai AB ir AC bus kojos, o šoninis BC - hipotenuzė. Taigi, pagal apibrėžimą kampo B sinusas yra lygus AC kojos santykiui su hipotenuzu: sinB = AC / BC, o kito kampo sinus C = AB / BC sinusas.

Dešiniuoju kampu trikampis - kampų funkcijospatogu apskaičiuoti: jokių papildomų konstrukcijų nereikia. Pakanka žinoti teisingų pusių ilgį. Tačiau dažniausiai žinoma tik dalis reikalingų duomenų, kitiems reikia ieškoti. Apsvarstykite, kaip tai padaryti.

Ieško sine du kojos

Mes paimame tą patį trikampio ABC tiesiniu kampu A, kuriame mes žinome kojų matmenis: AB = a, AC = c. Norėdami apskaičiuoti kampo C sinusą, reikia katetę padalinti į hipotenuzą:

• sinC = AB / BC = a / BC (1).

Tačiau hipotenuzą reikės atsižvelgti pagal Pitagoro teoremą:

• BC = √ (AB² + AC²) = √ (a² + b²). (2)

Mes pateikime rastą hipotenuzės (2) reikšmę išraiškoje (1), mes gauname atsakymą:

• sinC = a / √ (a² + b²).

Ieškote sinuso ant hipotenuzės ir šalia esančios kojos

Dabar toje pačioje trikampyje mes turime rasti tos pačios kampo C sinusą, bet mes žinome, kad hipotenuzė BC = b ir katodas AC = c. Pagal Pitagoro teoremą: AB² + AC² = BC² mes ieškome AB:

• AB = √ (b²-c²).

Dabar pakeiskite AB nustatytą reikšmę sinuso formulėje:

• sinC = AB / b = √ (b²-c²) / b.

Sine skaičiavimas vienoje pusėje ir aštriame kampe

Trikampyje ABC su dešiniuoju kampu A žinomas kampas B = β, o katetetas AC = c. Mums reikia rasti kampo C sinusą.

1 metodas.

Paprasčiausia - jei prisimenate, kad visų kampų trikampyje suma yra 180 °:

• A + B + C = 180 °.
• Kampas A = 90 °, B = β,
• C = 180 ° -90 ° - β = 90 ° - β.
• Taigi sinC = sin (90 ° - β).

2 metodas.

Bet jūs galite pereiti kitu būdu:

• Sinβ = AC / BC; Sinβ = c / BC. Iš čia:
• BC = c / Sinβ.

Iš Pythagoras AB2 + AC2 = BC2 teoremos mes nustatome hipotenuzą:

• AB = √ (BC²-AC²).

Mes pakeičiame žinomas vertes:

• AB = √ (с² / Sin²β-c²) = √с² (1 / Sin²β-1) = с√ (1 / Sin²β-1).

Taigi randame kampo C sinusą:

• Sinc = AB / BC = s√ (1 / Sin²β-1) / S / Sinβ = Sinβ √ (1 / Sin²β-1)

Atsakymas:

• sinC = Sinβ √ (1 / Sin²β-1).