Kaip rasti ūminį lygiagretainio kampą?

Lygiagrelis yra keturkampis, kuriame priešingos pusės yra poringos lygiagrečios.

Paralelograma turi visas keturkampių savybes, bet turi ir savo išskirtines savybes. Žinodami juos, mes galime lengvai rasti abi puses ir paralelografo kampus.

Parallelogram Properties

1. Kiekvienos lygiagrečios kampo, kaip ir bet kurio keturkampio, kampų suma yra 360 °.
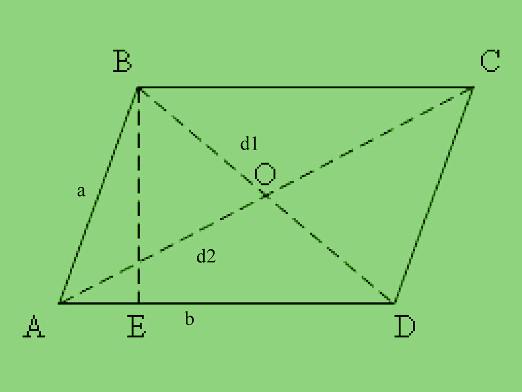
2. Paralelografo ir jo įstrižainės vidurinės linijos susikerta viename taške ir padalijamos pusiau. Šis taškas paprastai vadinamas lygiagretainio simetrijos centru.
3. Lygiagrečiosios pusės priešingos pusės visada lygios.
4. Taip pat šis skaičius visada turi priešingus kampus.
5. Kampų, besiribojančių abiejose paralelografo pusėse, suma visada yra 180 °.
6. Lygiagrečių įstrižainių kvadratų suma yra dvigubai didesnė už dviejų gretimų pusių kvadratų sumą. Tai išreiškiama pagal formulę:
   • d₁² + d₂² = 2 (a²+ b²), kur d₁ ir d₂ - įstrižainės, a ir b - gretimos pusės.
7. Tuščio kampo kosinusas visada yra mažesnis nei nulis.

Kaip rasti tam tikro paralelografo kampuspraktiškai pritaikyti šias savybes? O kokios kitos formulės mums gali padėti? Pažvelkime į konkrečias užduotis, kurių reikia: suraskite paralelografo kampus.

Paralelografo kampų paieška

1 atvejis. Yra žinoma, kad tukes kampas yra matuojamas, todėl reikia rasti ūminį kampą.

Pavyzdys: lygiagrečiame ABCD, kampas A yra 120 °. Rasti kitų kampų matą.

Sprendimas: Naudodamiesi nuosavybe Nr. 5, mes galime rasti kampo B matą greta problemos nurodyto kampo. Tai bus lygus:

• 180 ° -120 ° = 60 °

Ir dabar, naudojant nuosavybės numerį 4, mes nustatome,kad du likę kampai C ir D yra priešingi tiems, kuriuos jau rastume. Kampas C yra priešingas kampui A, kampas D iki kampo B. Todėl jie yra lygiaverčiai jiems.

• Atsakymas: B = 60 °, C = 120 °, D = 60 °

2 atvejis. Žinomos pusės ir įstrižainės

Šiuo atveju turime naudoti kosinusinę teoremą.

Mes galime pirmiausia apskaičiuoti kampą, reikalingą iš formulės, cosinusą ir tada iš specialios lentelės sužinoti, koks yra pats kampas.

Dėl ūmaus kampo formulė yra:

• cosa = (А² + В² - d²) / (2 * А * В), kur
• a yra norimas ūminis kampas,
• A ir B yra lygiagrečiosios pusės,
• D - mažesnė įstrižainė

Tuščia kampo formulė šiek tiek keičia:

• cosß = (А² + В² - D²) / (2 * А * В), kur
• ß yra tukes kampas
• A ir B yra pusės,
• D - didelė įstrižainė

Pavyzdys: rasti smailų lygiagretainio kurio kraštinės yra 3 cm ir 6 cm ir mažesnis įstrižainės yra 5,2 cm

Pakeiskite formulės vertes, kad rastumėte ūminį kampą:

• cosa = (6² + 3² - 5.2²) / (2 * 6 * 3) = (36 + 9 - 27,04) / (2 * 18) = 17,96 / 36 ~ 18/36 ~ 1/2
• cosa = 1/2. Pagal lentelę matome, kad reikalingas kampas yra 60 °.
• Atsakymas: 60 °