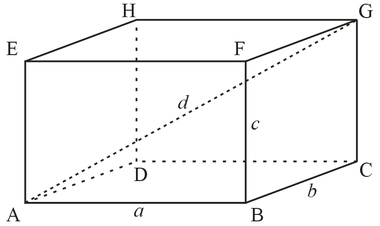
Kaip rasti kūgio aukštį?

Kūgis yra smailas paveikslas, prie pagrindokuris yra ratas. Iš išorės jis panašus į gaubtą. Aukštis yra statmenas, nukritęs nuo viršaus iki kūgio pagrindo. Linija, jungianti kūgio viršūnę su pagrindu ir ištraukta statmenai pagrindo plokštumai, vadinama generatoriumi.

Mes randame kūgio aukštį: sprendimo algoritmą

Jei kyla klausimas, kaip rasti kūgio aukštį, mes padėsime tinkamo trikampio savybėms:

1. Pihagoros teorema (kryžminė hipotenuzė yra lygi kojų kvadratų sumai).
2. Kampų ir hipotenozės kampų priklausomybė: kampo sinusas yra lygus priešingos kojos ir hipotenelio santykiui; Kampo kosinizė yra lygi gretimos kojos ir hypotenuzės santykiui.

Problemų sprendimo algoritmas kūgio aukštyje yra toks:

1. Nubraukite kūgį, atkreipkite aukštį, pažymėkite visus žinomus duomenis.
2. Rasti stačiakampį trikampį, kurį sudaro aukštis ir problemos duomenys pagal segmentus ir kampus. Jei jis netrukus išsivers, atlikite papildomas konstrukcijas.
3. Taikant formulės dešiniam trikampiui, suraskite aukštį.

Kaip rasti kūgio aukštį: pavyzdžiai

Rasti tiesaus kūgio aukštį

Jei statmena nukrito nuo kūgio viršūnėsant jo pagrindo patenka į apskritimo centrą, kūgis vadinamas tiesia linija. Taigi, turime kūgį su generatoriu l = 16. Kampas tarp generatoriaus ir pagrindo yra 30 °.

1. Mes pagaminsime tiesinį kūgį, kurio formos aukštis.
2. Centras jungiame prie aukščio ir formavimo spindulio pabaigos. Aukštis h ir pagrindo spindulys yra dešinio kampo trikampio kojos, formuojančios hipotenuzą.
3. Kampo sine nuo hypotenuse-generatrix ir pagrindo pėdos spindulio yra nuodėmė 30 ° = ½. Šis priešingos kojos santykis - aukštis h - ir hypotenuse:
   • sin 30 ° = h / l = ½
   • h = sin 30 ° * l = ½ * 16 = 8.

Kaip rasti sutrumpinto kūgio aukštį

Trumpas kūgis gaunamas, jei įprastasKūgis iškirptas viršuje. Mes imkime tiesinį sutrumpintą kūgį. Viršutinės bazės skersmuo yra d = 2, apatinės pagrindo skersmuo yra D = 4, sudarant l = 4. Mums reikia rasti kūgio h aukštį, t. Y. atstumas tarp dviejų

pagrindai.

1. Mes nupiešome sutrumpintą kūgį. Trumpojo kūgio vertikalusis skerspjūvis yra lygumoje esantis trapecijos ir problema turi būti išspręsta kaip trapecijos problema.
2. Pažvelkime į trikampį iš aukščio, kuris sudaro skersmens a segmentą, kuris yra skirtumas tarp apatinio ir viršutinio skersmens, padalintų iš dviejų: a = (D-d) / 2 = (4 - 2) / 2 = 1.
3. Skersmens segmentas - katetas, aukštis h - antroji kojelė - yra lygus hipotūnio ir kojos kyšių (Pythagoras teorema) skirtumo šakniui:
   • h = √ (² - a ²) = √ (4 ² - 1 ²) = √15.
   • Atsakymas: h = √15.

Kaip rasti savavališko kūgio aukštį

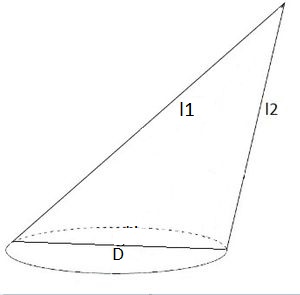
Tarkime, kad turime savavališką kūgį subazė apskritimo forma. Kūgio viršūnė tęsiasi už pagrindo. Vertikaliąją dalį kertanti viršūnės ir pagrindo skersmuo yra atitveria buką trikampis: du generatoriai 8 ir L1 = L2 = 3 ir skersmuo D = 5. aukštis h, sumažino iš viršaus, patenka nuo tolesnio skersmens. Būtina rasti aukštį h.

Atstumas nuo bumuoto kampo viršūnės iki skersmens ir jo aukščio sankirtos taško žymimas x. Mes gauname du stačiakampius trikampius:

1. Generatorius l1 - skersmuo ir segmentas x - aukštis
2. Generatrix l2 yra segmentas x yra aukštis.

Mes įrašome, kas yra aukščiausiasis Pihagoros teoremas:

• h² = l1² - (D + x) ² (1)
• h² = l2² - x² (2)

Gauta dviejų lygčių sistema, o dešiniosios pusės šių lygčių yra lygios h 2 ir yra vienodos:

• l1² - (D + x) ² = l2² - x²

Išplečiame skliaustus:

• l1² - D² - 2 D x - x² = l2² - x²

Sutrumpinkite x²:

• l1² - D² - 2 D x = l2²
• 2D x = l2² - l1² + D²
• x = (l2² - l1² + D²) / 2D = (8² - 5² - 3²) / 5 = 2 * (64 - 25-9) / 10 = 3.

Mes pakeičia x į išraišką (2), mes randame h:

• h² = l2² - x²
• h = √ (l2² - x²) = √ (25 - 9) = 4
• Atsakymas: h = 4