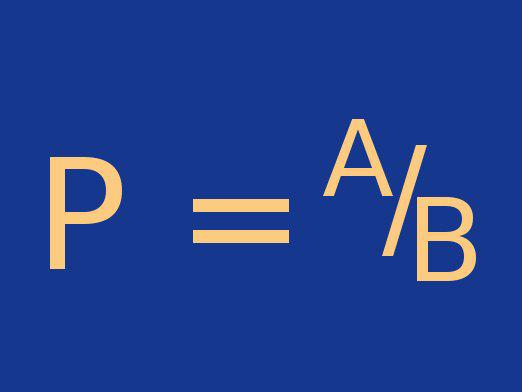Kaip išspręsti tikimybės problemą?

Tikimybių teorija yra gana didelėnepriklausoma matematikos šaka. Mokyklų kurse tikimybių teorija laikoma labai paviršutiniška, tačiau USE ir GIA yra šios temos užduotys. Tačiau, siekiant išspręsti mokyklos žinoma problema yra ne per sunku (bent jau tai, kas susijęs su aritmetinės operacijos) - nėra būtinybės nagrinėti dariniai, integralai ir imtis spręsti sudėtingas trigonometrines transformacijas - svarbiausia, kad būtų galima dirbti paprastus numerius ir jų frakcijos.

Tikimybių teorija - pagrindiniai terminai

Pagrindinės tikimybių teorijos sąlygos yra testavimas,rezultatas ir atsitiktinis įvykis. Tikimybių teorijos testas yra eksperimentas - išmesti monetą, parengti kortelę, nubėgti išmesti - visa tai yra testas. Testo rezultatas, kaip jau spėjote, vadinamas rezultatu.

Ir koks įvykio atsitiktinumas? Tikimybių teorijoje daroma prielaida, kad bandymas atliekamas ne vieną kartą ir yra daug rezultatų. Atsitiktinis įvykis yra bandymų rezultatų rinkinys. Pavyzdžiui, jei įmetate monetą, gali būti du atsitiktiniai įvykiai - erelis ar uodegos paliks.

Negalima supainioti rezultatų ir atsitiktinių įvykių sąvokos. Rezultatas yra vienas iš bandymų rezultatų. Atsitiktinis įvykis yra galimų rezultatų rinkinys. Beje, taip pat yra tokio termino kaip neįmanoma įvykis. Pavyzdžiui, įvykis "numetė skaičių 8" į standartines žaidimo kauliukas neįmanomas.

Kaip rasti tikimybę?

Mes visi grubiai suprantame, kokia yra tikimybė,ir gana dažnai mes naudojame šį žodį mūsų leksikone. Be to, mes netgi galime padaryti tam tikras išvadas apie įvykio tikimybę, pavyzdžiui, esant sniege už lango, mes dažniau sakome, kad dabar nėra vasaros. Tačiau kaip išreikšti šią prielaidą skaičiais?

Norint pateikti formulę rastitikimybe pristatome dar vieną koncepciją - palankų rezultatą, tai yra rezultatas, palankus tam tikram įvykiui. Žinoma, apibrėžtis yra gana dviprasmiška, tačiau problemos būklė visada aiški, kokie rezultatai yra palankūs.

Pavyzdžiui: klasėje yra 25 žmonės, iš kurių trys yra Katie. Mokytojas skiria pareigą Oli, ir jai reikia partnerio. Kokia yra tikimybė, kad Katya taps partneriu?

Šiame pavyzdyje palankus rezultatas - partneris Katja. Šiek tiek vėliau mes išspręstume šią problemą. Bet pirmiausia, naudodamiesi papildomu apibrėžimu, mes pateikiame formulę norint rasti tikimybę.

• P = A / N, kur P - tikimybė, A - palankių rezultatų skaičius, N - bendras rezultatų skaičius.

Visos šios mokyklos užduotys apsunkina šią formulę, o pagrindinis sunkumas paprastai yra rezultatų. Kartais juos lengva rasti, kartais ne.

Kaip išspręsti tikimybės problemą?

1 užduotis

Taigi, dabar išspręskime pirmiau minėtą problemą.

Palankių rezultatų skaičius (mokytojas pasirinksKatya) yra lygus trims, nes klasėje yra 3 trys, o bendras rezultatas yra 24 (25-1, nes jau yra parinkta Olya). Tada tikimybė yra: P = 3/24 = 1/8 = 0,125. Taigi tikimybė, kad "Katya" partneris bus "Katya", yra 12,5%. Tai lengva, tiesa? Pažvelkime į kažką sudėtingesnį.

2 užduotis

Moneta buvo išmesta du kartus, kokia tikimybė, kad derinys sumažės: vienas erelis ir vienas uodegos?

Taigi, mes vertiname bendrus rezultatus. Kaip gali išeiti monetos-erelis / erelis, uodegos / uodegos, erelis / uodegos, uodegos / erelis? Taigi bendras rezultatų skaičius yra 4. Kiek palankių rezultatų? Du - erelis / uodegos ir uodegos / erelis. Taigi, erelio ar uodegos derinio tikimybė yra tokia:

• P = 2/4 = 0,5 arba 50 proc.

Ir dabar mes manome, kad tokia problema. Masoje yra 6 monetos kišenėje: dvi - nominali vertė 5 rubliai ir keturi - nominali vertė 10 rublių. Masha perkėlė 3 monetas į kitą kišenę. Kokia tikimybė, kad 5 rublių monetos bus skirtingose ​​kišenėse?

Paprastumui įvardinkime monetas skaitmenyse - 1,2 - penkių rublių monetų, 3,4,5,6 - dešimties rublių monetų. Taigi, kaip monetos gali būti jūsų kišenėje? Yra 20 derinių:

• 123, 124, 125, 126, 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256, 345, 346, 356, 456.

Iš pirmo žvilgsnio gali atrodyti, kad kai kurie deriniai išnyko, pavyzdžiui, 231, bet mūsų atveju 123, 231 ir 321 deriniai yra lygiaverčiai.

Dabar svarstome, kiek palankiosrezultatai. Juos priimti tuos derinius, kur yra arba 1 pav arba 2 paveikslas: 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256. Jų 12. Taigi, tikimybė yra:

• P = 12/20 = 0,6 arba 60%.

Problemos, susijusios su tikimybių teorijaČia gana paprasta, bet nemanau, kad tikimybių teorija yra paprastas matematikos skyrius. Jei nuspręsite tęsti studijas universitete (išskyrus humanitarines specialybes), jūs tikrai turėsite poras aukštojoje matematikos srityje, kur jums bus pristatomi sudėtingesni teorijos terminai, o užduotis bus sunkiau.

Taip pat skaitykite straipsnį Kaip apskaičiuoti tikimybę.